分卷阅读45
角函数与
术也存在关系。术绘画中最基础的
相环就是一个圆形，从红开始各种颜
据调的冷
度均匀的分布在整个圆环上，每种系有其特定的弧度范围，据圆周角度的大小可以准确的判断
互补、对比、邻近和类似。
涂化和沈思易对视一
，这个沈思易果然深不可测，短短几分钟的时间，他竟然能将这么多旁人难以注意到的信息以这种九曲回
的方式联系起来，他的思维能力和逻辑能力的确令人难以望其项背。
这么一来，涂化就明白了，所有的条件都在指向同一个答案：“粉石台上的数字应该是2。”
站在粉石台上的唐博却不太明白：“为什么？”
所以这个圆弦七星阵将三原设置在圆周上不无
理，系统正是想将缤纷的颜与三角函数联系起来。
角函数与术也存在关系。术绘画中最基础的相环就是一个圆形，从红开始各种颜据调的冷度均匀的分布在整个圆环上，每种系有其特定的弧度范围，据圆周角度的大小可以准确的判断互补、对比、邻近和类似。
所以这个圆弦七星阵将三原设置在圆周上不无理，系统正是想将缤纷的颜与三角函数联系起来。
“可你说的这个规律最多只能算颜与三角函数的规律，和石台上的数字是没有关联的。”孙维疑惑，“单凭这一
就判断粉石台等于2会不会太草率了？”
沈思易接着涂化的分析：“数字之间也是存在规律的，你记得我刚开始说的在同一直线上的黄6白3=淡黄3的2次方这件事
吗？淡蓝石台上1就是1的1次方。”
涂化和沈思易对视一，这个沈思易果然深不可测，短短几分钟的时间，他竟然能将这么多旁人难以注意到的信息以这种九曲回的方式联系起来，他的思维能力和逻辑能力的确令人难以望其项背。
“淡蓝、粉、淡黄这三个石台不单单是代表的数字存在顺序关系，它们所在的直线运算中也是存在顺序的。”沈思易，“
照红黄蓝三原的顺序，红对应的粉石台上的数字在运算时表示3次幂，也就是说粉石台上2这个数字的三次方等于8，红石台数
“淡蓝、粉、淡黄这三个石台不单单是代表的数字存在顺序关系，它们所在的直线运算中也是存在顺序的。”沈思易，“照红黄蓝三原的顺序，红对应的粉石台上的数字在运算时表示3次幂，也就是说粉石台上2这个数字的三次方等于8，红石台数
这么一来，涂化就明白了，所有的条件都在指向同一个答案：“粉石台上的数字应该是2。”
“可你说的这个规律最多只能算颜与三角函数的规律，和石台上的数字是没有关联的。”孙维疑惑，“单凭这一就判断粉石台等于2会不会太草率了？”
涂化和沈思易对视一，这个沈思易果然深不可测，短短几分钟的时间，他竟然能将这么多旁人难以注意到的信息以这种九曲回的方式联系起来，他的思维能力和逻辑能力的确令人难以望其项背。
“可你说的这个规律最多只能算颜与三角函数的规律，和石台上的数字是没有关联的。”孙维疑惑，“单凭这一就判断粉石台等于2会不会太草率了？”
所以这个圆弦七星阵将三原设置在圆周上不无理，系统正是想将缤纷的颜与三角函数联系起来。
“不论是我们
格
的顺序还是三原的顺序，都是以红为起的，那么在三角函数的角度中，我同样应该以红的这条边为起。”他用手比划着红石台与白石台之间相连的这条直线，“以红白这条直线为起，在圆周上，红石台所在的角度为0度，黄石台所在的角度，也就是沈思易刚刚说的红白黄这个夹角，为60度；同理，蓝所在的角度为120度。”
沈思易赞许地看着他。
⋍奲ꐬ﬩롑४dzꞒ氃厴픈ﵱ늂ԡⰴᤨ䖣봬涂化和沈思易对视一，这个沈思易果然深不可测，短短几分钟的时间，他竟然能将这么多旁人难以注意到的信息以这种九曲回的方式联系起来，他的思维能力和逻辑能力的确令人难以望其项背。
沈思易接着涂化的分析：“数字之间也是存在规律的，你记得我刚开始说的在同一直线上的黄6白3=淡黄3的2次方这件事吗？淡蓝石台上1就是1的1次方。”
涂化和沈思易对视一，这个沈思易果然深不可测，短短几分钟的时间，他竟然能将这么多旁人难以注意到的信息以这种九曲回的方式联系起来，他的思维能力和逻辑能力的确令人难以望其项背。
“淡蓝、粉、淡黄这三个石台不单单是代表的数字存在顺序关系，它们所在的直线运算中也是存在顺序的。”沈思易，“照红黄蓝三原的顺序，红对应的粉石台上的数字在运算时表示3次幂，也就是说粉石台上2这个数字的三次方等于8，红石台数
这么一来，涂化就明白了，所有的条件都在指向同一个答案：“粉石台上的数字应该是2。”
站在粉石台上的唐博却不太明白：“为什么？”
站在粉石台上的唐博却不太明白：“为什么？”
涂化指着与黄和蓝
在同一条直线上的淡黄和淡蓝石台，：“恰巧可以发现，与排在第1位的蓝对应的淡蓝石台上的数字正好是1，排在第3位的黄石台相对应的淡黄石台上的数字正好就是3。”
在他的提之
，涂化才想明白了其中缘由：“红、黄、蓝三原的地位就像正弦、余弦、正切三个初等函数在三角函数中的地位，最基础，也是所有相和函数变换的源。”涂化伸手指着自己脚的红石台，“所以我们可以
行类比，红代表的就是正弦sin，黄代表余弦cos，蓝代表正切tan。”
站在粉石台上的唐博却不太明白：“为什么？”
站在粉石台上的唐博却不太明白：“为什么？”
涂化和沈思易对视一，这个沈思易果然深不可测，短短几分钟的时间，他竟然能将这么多旁人难以注意到的信息以这种九曲回的方式联系起来，他的思维能力和逻辑能力的确令人难以望其项背。
涂化指着与黄和蓝在同一条直线上的淡黄和淡蓝石台，：“恰巧可以发现，与排在第1位的蓝对应的淡蓝石台上的数字正好是1，排在第3位的黄石台相对应的淡黄石台上的数字正好就是3。”
站在粉石台上的唐博却不太明白：“为什么？”
“可你说的这个规律最多只能算颜与三角函数的规律，和石台上的数字是没有关联的。”孙维疑惑，“单凭这一就判断粉石台等于2会不会太草率了？”
站在粉石台上的唐博却不太明白：“为什么？”
“不论是我们格的顺序还是三原的顺序，都是以红为起的，那么在三角函数的角度中，我同样应该以红的这条边为起。”他用手比划着红石台与白石台之间相连的这条直线，“以红白这条直线为起，在圆周上，红石台所在的角度为0度，黄石台所在的角度，也就是沈思易刚刚说的红白黄这个夹角，为60度；同理，蓝所在的角度为120度。”
在他的提之，涂化才想明白了其中缘由：“红、黄、蓝三原的地位就像正弦、余弦、正切三个初等函数在三角函数中的地位，最基础，也是所有相和函数变换的源。”涂化伸手指着自己脚的红石台，“所以我们可以行类比，红代表的就是正弦sin，黄代表余弦cos，蓝代表正切tan。”
“可你说的这个规律最多只能算颜与三角函数的规律，和石台上的数字是没有关联的。”孙维疑惑，“单凭这一就判断粉石台等于2会不会太草率了？”
“淡蓝、粉、淡黄这三个石台不单单是代表的数字存在顺序关系，它们所在的直线运算中也是存在顺序的。”沈思易，“照红黄蓝三原的顺序，红对应的粉石台上的数字在运算时表示3次幂，也就是说粉石台上2这个数字的三次方等于8，红石台数
角函数与术也存在关系。术绘画中最基础的相环就是一个圆形，从红开始各种颜据调的冷度均匀的分布在整个圆环上，每种系有其特定的弧度范围，据圆周角度的大小可以准确的判断互补、对比、邻近和类似。
“刚刚说过，红、黄、蓝三分别代表正弦sin、余弦cos、正切tan，我们只要把它们相对应的角度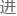行三角函数赋值就会发现，sin0=0，cos60=1/2，tan120=负的号3。”涂化分析，“把这三个三角函数的赋值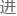行对比可以发现，tan120＜sin0＜cos60，照这个顺序给他们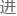行排序就会发现蓝的tan120是最小的，排在第1位，红sin0是第2位，黄的cos60是最大的也就是第3位。”
沈思易接着涂化的分析：“数字之间也是存在规律的，你记得我刚开始说的在同一直线上的黄6白3=淡黄3的2次方这件事吗？淡蓝石台上1就是1的1次方。”
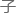“不论是我们格的顺序还是三原的顺序，都是以红为起的，那么在三角函数的角度中，我同样应该以红的这条边为起。”他用手比划着红石台与白石台之间相连的这条直线，“以红白这条直线为起，在圆周上，红石台所在的角度为0度，黄石台所在的角度，也就是沈思易刚刚说的红白黄这个夹角，为60度；同理，蓝所在的角度为120度。”
涂化和沈思易对视一，这个沈思易果然深不可测，短短几分钟的时间，他竟然能将这么多旁人难以注意到的信息以这种九曲回的方式联系起来，他的思维能力和逻辑能力的确令人难以望其项背。
沈思易赞许地看着他。
⋍奲ꐬ﬩롑४dzꞒ氃厴픈ﵱ늂ԡⰴᤨ䖣봬“刚刚说过，红、黄、蓝三分别代表正弦sin、余弦cos、正切tan，我们只要把它们相对应的角度行三角函数赋值就会发现，sin0=0，cos60=1/2，tan120=负的号3。”涂化分析，“把这三个三角函数的赋值行对比可以发现，tan120＜sin0＜cos60，照这个顺序给他们行排序就会发现蓝的tan120是最小的，排在第1位，红sin0是第2位，黄的cos60是最大的也就是第3位。”
所以这个圆弦七星阵将三原设置在圆周上不无理，系统正是想将缤纷的颜与三角函数联系起来。
“淡蓝、粉、淡黄这三个石台不单单是代表的数字存在顺序关系，它们所在的直线运算中也是存在顺序的。”沈思易，“照红黄蓝三原的顺序，红对应的粉石台上的数字在运算时表示3次幂，也就是说粉石台上2这个数字的三次方等于8，红石台数
“刚刚说过，红、黄、蓝三分别代表正弦sin、余弦cos、正切tan，我们只要把它们相对应的角度行三角函数赋值就会发现，sin0=0，cos60=1/2，tan120=负的号3。”涂化分析，“把这三个三角函数的赋值行对比可以发现，tan120＜sin0＜cos60，照这个顺序给他们行排序就会发现蓝的tan120是最小的，排在第1位，红sin0是第2位，黄的cos60是最大的也就是第3位。”
涂化指着与黄和蓝在同一条直线上的淡黄和淡蓝石台，：“恰巧可以发现，与排在第1位的蓝对应的淡蓝石台上的数字正好是1，排在第3位的黄石台相对应的淡黄石台上的数字正好就是3。”
“淡蓝、粉、淡黄这三个石台不单单是代表的数字存在顺序关系，它们所在的直线运算中也是存在顺序的。”沈思易，“照红黄蓝三原的顺序，红对应的粉石台上的数字在运算时表示3次幂，也就是说粉石台上2这个数字的三次方等于8，红石台数
所以这个圆弦七星阵将三原设置在圆周上不无理，系统正是想将缤纷的颜与三角函数联系起来。
涂化指着与黄和蓝在同一条直线上的淡黄和淡蓝石台，：“恰巧可以发现，与排在第1位的蓝对应的淡蓝石台上的数字正好是1，排在第3位的黄石台相对应的淡黄石台上的数字正好就是3。”
这么一来，涂化就明白了，所有的条件都在指向同一个答案：“粉石台上的数字应该是2。”
涂化指着与黄和蓝在同一条直线上的淡黄和淡蓝石台，：“恰巧可以发现，与排在第1位的蓝对应的淡蓝石台上的数字正好是1，排在第3位的黄石台相对应的淡黄石台上的数字正好就是3。”
涂化指着与黄和蓝在同一条直线上的淡黄和淡蓝石台，：“恰巧可以发现，与排在第1位的蓝对应的淡蓝石台上的数字正好是1，排在第3位的黄石台相对应的淡黄石台上的数字正好就是3。”
涂化指着与黄和蓝在同一条直线上的淡黄和淡蓝石台，：“恰巧可以发现，与排在第1位的蓝对应的淡蓝石台上的数字正好是1，排在第3位的黄石台相对应的淡黄石台上的数字正好就是3。”
“不论是我们格的顺序还是三原的顺序，都是以红为起的，那么在三角函数的角度中，我同样应该以红的这条边为起。”他用手比划着红石台与白石台之间相连的这条直线，“以红白这条直线为起，在圆周上，红石台所在的角度为0度，黄石台所在的角度，也就是沈思易刚刚说的红白黄这个夹角，为60度；同理，蓝所在的角度为120度。”
所以这个圆弦七星阵将三原设置在圆周上不无理，系统正是想将缤纷的颜与三角函数联系起来。
涂化指着与黄和蓝在同一条直线上的淡黄和淡蓝石台，：“恰巧可以发现，与排在第1位的蓝对应的淡蓝石台上的数字正好是1，排在第3位的黄石台相对应的淡黄石台上的数字正好就是3。”
“可你说的这个规律最多只能算颜与三角函数的规律，和石台上的数字是没有关联的。”孙维疑惑，“单凭这一就判断粉石台等于2会不会太草率了？”
沈思易赞许地看着他。
⋍奲ꐬ﬩롑४dzꞒ氃厴픈ﵱ늂ԡⰴᤨ䖣봬“淡蓝、粉、淡黄这三个石台不单单是代表的数字存在顺序关系，它们所在的直线运算中也是存在顺序的。”沈思易，“照红黄蓝三原的顺序，红对应的粉石台上的数字在运算时表示3次幂，也就是说粉石台上2这个数字的三次方等于8，红石台数
站在粉石台上的唐博却不太明白：“为什么？”
“刚刚说过，红、黄、蓝三分别代表正弦sin、余弦cos、正切tan，我们只要把它们相对应的角度行三角函数赋值就会发现，sin0=0，cos60=1/2，tan120=负的号3。”涂化分析，“把这三个三角函数的赋值行对比可以发现，tan120＜sin0＜cos60，照这个顺序给他们行排序就会发现蓝的tan120是最小的，排在第1位，红sin0是第2位，黄的cos60是最大的也就是第3位。”
涂化和沈思易对视一，这个沈思易果然深不可测，短短几分钟的时间，他竟然能将这么多旁人难以注意到的信息以这种九曲回的方式联系起来，他的思维能力和逻辑能力的确令人难以望其项背。
沈思易接着涂化的分析：“数字之间也是存在规律的，你记得我刚开始说的在同一直线上的黄6白3=淡黄3的2次方这件事吗？淡蓝石台上1就是1的1次方。”
角函数与术也存在关系。术绘画中最基础的相环就是一个圆形，从红开始各种颜据调的冷度均匀的分布在整个圆环上，每种系有其特定的弧度范围，据圆周角度的大小可以准确的判断互补、对比、邻近和类似。
“刚刚说过，红、黄、蓝三分别代表正弦sin、余弦cos、正切tan，我们只要把它们相对应的角度行三角函数赋值就会发现，sin0=0，cos60=1/2，tan120=负的号3。”涂化分析，“把这三个三角函数的赋值行对比可以发现，tan120＜sin0＜cos60，照这个顺序给他们行排序就会发现蓝的tan120是最小的，排在第1位，红sin0是第2位，黄的cos60是最大的也就是第3位。”
“刚刚说过，红、黄、蓝三分别代表正弦sin、余弦cos、正切tan，我们只要把它们相对应的角度行三角函数赋值就会发现，sin0=0，cos60=1/2，tan120=负的号3。”涂化分析，“把这三个三角函数的赋值行对比可以发现，tan120＜sin0＜cos60，照这个顺序给他们行排序就会发现蓝的tan120是最小的，排在第1位，红sin0是第2位，黄的cos60是最大的也就是第3位。”
所以这个圆弦七星阵将三原设置在圆周上不无理，系统正是想将缤纷的颜与三角函数联系起来。
这么一来，涂化就明白了，所有的条件都在指向同一个答案：“粉石台上的数字应该是2。”
“淡蓝、粉、淡黄这三个石台不单单是代表的数字存在顺序关系，它们所在的直线运算中也是存在顺序的。”沈思易，“照红黄蓝三原的顺序，红对应的粉石台上的数字在运算时表示3次幂，也就是说粉石台上2这个数字的三次方等于8，红石台数
所以这个圆弦七星阵将三原设置在圆周上不无理，系统正是想将缤纷的颜与三角函数联系起来。
涂化指着与黄和蓝在同一条直线上的淡黄和淡蓝石台，：“恰巧可以发现，与排在第1位的蓝对应的淡蓝石台上的数字正好是1，排在第3位的黄石台相对应的淡黄石台上的数字正好就是3。”
所以这个圆弦七星阵将三原设置在圆周上不无理，系统正是想将缤纷的颜与三角函数联系起来。
“不论是我们格的顺序还是三原的顺序，都是以红为起的，那么在三角函数的角度中，我同样应该以红的这条边为起。”他用手比划着红石台与白石台之间相连的这条直线，“以红白这条直线为起，在圆周上，红石台所在的角度为0度，黄石台所在的角度，也就是沈思易刚刚说的红白黄这个夹角，为60度；同理，蓝所在的角度为120度。”
“淡蓝、粉、淡黄这三个石台不单单是代表的数字存在顺序关系，它们所在的直线运算中也是存在顺序的。”沈思易，“照红黄蓝三原的顺序，红对应的粉石台上的数字在运算时表示3次幂，也就是说粉石台上2这个数字的三次方等于8，红石台数
【1】【2】
『加入书签，方便阅读』
